Our research builds the theoretical foundations for these settings. We analyse and develop distributed algorithms that are fast and communication efficient. Distributed algorithms are becoming increasingly important. Networks and the size of the data are often already too large to be stored, processed or controlled by a single central authority, or are distributed by design.
Benchmark Problem Graph Coloring
Let us illustrate this with an artificial example. Consider a large network of sensors deployed in the vineyards in the south of Styria that measure parameters such as temperature or humidity. Due to the steep nature of the vineyards, obstacles and limited battery capacity, these sensors cannot communicate to a central base station. Instead, they build a multihop network and a sensor only communicates with the sensors in its vicinity. Furthermore, their communication is wireless, so two close-by sensors cannot use the same frequency to send their messages, as otherwise interference might occur. Thus, our goal is to assign frequencies such that close-by sensors do not receive the same frequency. This can be modelled as a classic graph coloring problem. The network is abstracted as a graph where each vertex resembles a sensor and each edge between two vertices indicates that the two sensors are so close that they cannot use the same frequency. The objective is to assign a colour (= frequency) to each vertex such that neighbouring vertices receive different colours. To save resources, one desires to use as few colours as possible. Although so simple, graph coloring has played an influential role in computer science, maths and also in distributed computing. Computing an assignment using the minimal number of colours cannot be solved efficiently unless P = NP. In the distributed setting, we use more colours, but the problem still remains challenging. Recall our example. Each vertex of the graph is its own computer and does not know the network. How should one of these decide to use a specific colour without a central coordinator? Should it go for blue, red or green? It has to coordinate with its neighbours to not pick the same colour, and its neighbours have to coordinate with their neighbours, etc. Where do we begin? By rolling a dice.
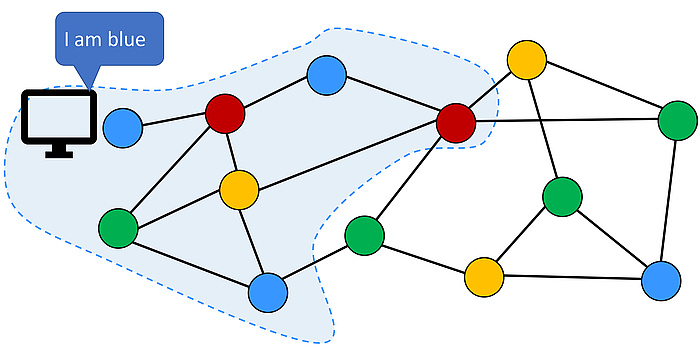
Figure 2: Networks are abstracted as graphs.
The Role of Randomness
Let each node simultaneously pick a random candidate colour by rolling a dice. If no neighbour tries the same candidate colour, stick to it, otherwise just roll the dice again. This is a simple and efficient algorithm. Unfortunately, its efficiency relies on having fair dices. Scientists call such algorithms randomized. Interestingly, many problems (not just the graph coloring problem) can be solved efficiently with randomization. Many of these have in common the fact that the correctness of a solution can be verified efficiently, e.g. you can ask your neighbour for its colour to see whether you have the same colour. But what if one wants so-called deterministic algorithms that do not use dices and are not only efficient if the “gods of the dices” are with us? Over the decades, the quest for efficient deterministic distributed algorithms has become the distributed version of the P vs. NP question: Can every problem whose solution can be verified efficiently by a distributed algorithm also be solved efficiently by a distributed algorithm? The classic P vs. NP question asks the same question for non-distributed algorithms. The answer to the distributed question is affirmative if we allow randomization. In order to also answer it for deterministic algorithms, we have built a large theory that relates randomized and deterministic complexities. Then, building on our theory, researchers from ETH Zurich have resolved the distributed P vs. NP question in the affirmative. Alas, these results come with expensive downsides; that is, they rely on a really large communication bandwidth in the network, something which is infeasible in practice.
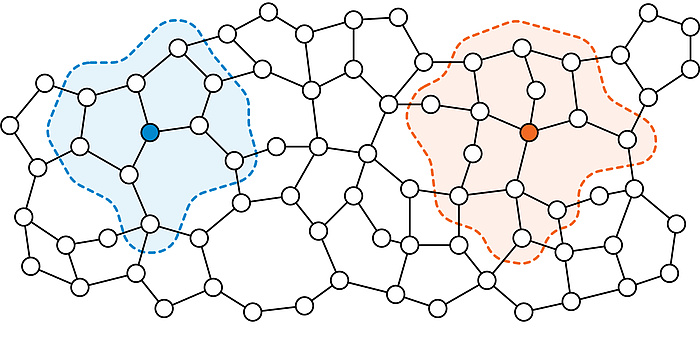
Figure 3: Classic distributed graph algorithms are allowed to use large messages and thus study the distance from which information in a graph has to be gathered to produce an output.
Communication Efficient and Simple Algorithms
Thus, in recent years we have successfully focused on the design of communication- and bandwidth-efficient algorithms. State-of-the-art algorithms are often very complicated and involved. Thus, besides being communication efficient and fast, one of our objectives is to design simple algorithms. Staying with our graph coloring example, we have shown that small changes to the aforementioned “roll-adice” algorithm suffice to make it exponentially faster.
Massively Parallel Computing
In large graph-processing frameworks, such as Google’s MapReduce or the opensource version Hadoop, a huge graph is arbitrarily distributed on a cluster of machines that communicate with each other in an all-to-all fashion. So, in contrast to the previous setting, there is no relation between the communication network and the input. Surprisingly, insights from network algorithms are very helpful in these frameworks, e.g. our communicationefficient algorithms are robust and run in such settings.
Algorithmic Challenges in our Modern World
Our future research will build foundations for the emerging algorithmic challenges in our modern world, e.g. the design of streaming and sublinear algorithms. Most real-world graphs are non-static in nature, e.g. the Facebook graph keeps changing when new users join or leave the network. We aim to design dynamic algorithms that react quickly to changes without recomputing solutions from scratch. The impact of distributed computing in these areas has been growing and new connections are being drawn each day.
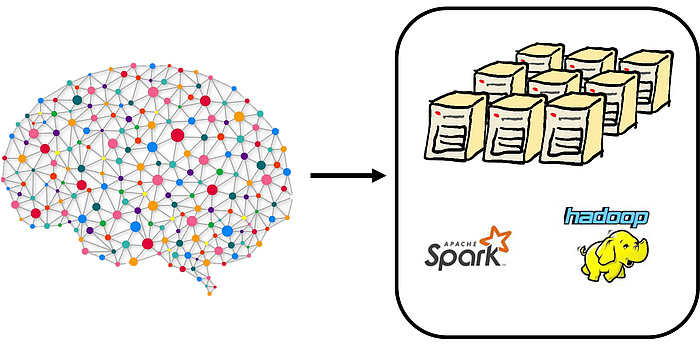
Figure 4: The figure shows the massively parallel computing framework to which network algorithms contribute.

