Elektrische Maschinen sind heutzutage in unserem Leben allgegenwärtig. Um Maschinen zu gestalten, die – je nach konkreter Anwendung – ihre Aufgaben so gut wie möglich erfüllen, können Verfahren zur mathematischen Optimierung der Geometrie der Maschinen verwendet werden. Solche Verfahren können auch zu neuen Designs führen, die man so eventuell nicht erwartet hätte.
Elektrische Maschinen sind aus unserem täglichen Leben nicht mehr wegzudenken. Immer wenn wir einen Stecker in die Steckdose stecken und dadurch ein Gerät in Bewegung versetzen – sei es ein Mixer, ein Staubsauger oder eine Waschmaschine –, ist ein Elektromotor im Spiel (siehe Abbildung 1), der elektrische Energie in mechanische Energie umwandelt. Auch in industriellen Anwendungen sind Elektromotoren weitgehend unverzichtbar, Industrie-Elektromotoren verbrauchen sogar mehr als 40 Prozent der weltweit produzierten elektrischen Energie. Es ist also offensichtlich, dass die Optimierung solcher elektrischen Maschinen ein großes Potenzial zur Einsparung von Energie darstellt.
Bei der Auslegung elektrischer Motoren muss neben grundsätzlichen Fragen wie nach der Art, Größe oder nach den verwendeten Materialien auch die genaue Gestalt des Motors bestimmt werden, die einen idealen Magnetfluss erlaubt. Da der Magnetfluss im Eisen besser ist als in Luftbereichen des Motors, kann man ihn durch geschicktes Einfügen von Löchern bzw. Luftbereichen in eine gewünschte Richtung leiten (siehe Abbildung 2) und so das gesamte Verhalten des Elektromotors verändern. Dieser Designprozess geschieht häufig durch Intuition und Erfahrung von Elektroingenieur/innen. Durch nachträgliche Optimierung bezüglich geometrischer Parameter wie Längen oder Orientierung von Teilen des Motors kann dieser weiterverbessert werden. Hierbei können jedoch nur Designs erhalten werden, die dieselbe Gestalt haben wie das gewählte Anfangsdesign.
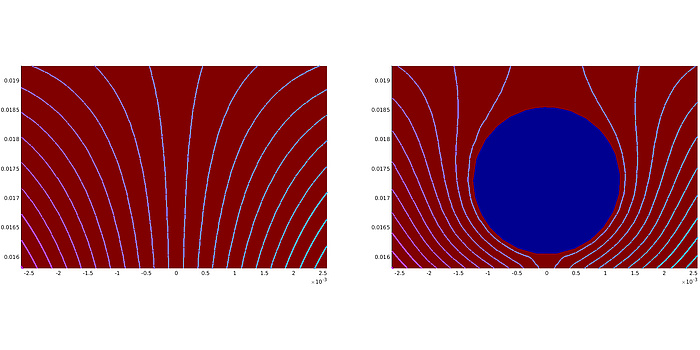
Abbildung 2: Magnetfluss in Eisen ohne und mit Lufteinschluss.
In meiner Forschung beschäftige ich mich mit der Frage, wie man die Lufteinschlüsse (beziehungsweise die Materialverteilung) in einem Motor in einer optimalen Art wählen kann, beispielsweise so, dass der Motor ein möglichst hohes mittleres Drehmoment oder eine möglichst hohe Laufruhe besitzt. Hierbei sollen keine Restriktionen an die Form und Anzahl der Lufteinschlüsse gesetzt werden, sodass auch neue, innovative Designs erzielt werden können. Diese praktische Aufgabenstellung lässt sich als ein mathematisches Problem der Form- bzw. Topologieoptimierung formulieren. Es geht also darum, die Gestalt eines Gebiets Ω (also eines gewissen Teils des Elektromotors) zu finden, für die eine gewisse Zielfunktion (zum Beispiel Drehmoment oder Laufruhe) maximiert wird.
In diesem Optimierungsproblem ist die Unbekannte also nicht ein Vektor von reellen Zahlen oder eine Funktion in einem Funktionenraum, sondern eine Menge Ω, die die Geometrie eines Teils des Motors repräsentiert (siehe Abbildung 3, links). Insbesondere liegt in diesem Fall keine Vektorraumstruktur vor, wir können also beispielsweise nicht zwei Mengen addieren oder subtrahieren. Um gradienten-basierte Optimierungsverfahren verwenden zu können, benötigen wir jedenfalls Ableitungsinformation, also Information über die Änderung der Zielfunktion bei einer Änderung der Menge Ω. Wir unterscheiden zwei Arten von Geometrieänderungen: einerseits die Verformung des Randes eines Gebiets in Richtung eines Vektorfelds (siehe Abbildung 3, Mitte) und andererseits die Veränderung der Geometrie durch Einfügen eines Loches im Inneren (siehe Abbildung 3, rechts). Die entsprechenden Ableitungsinformationen heißen Formableitung beziehungsweise topologische Ableitung. Mithilfe dieser Informationen ist es nun möglich, ähnlich wie bei einem Gradientenverfahren, schrittweise die Geometrie zu verbessern, bis man ein (lokal) optimales Design erreicht hat. In der Topologieoptimierung könnte man beispielsweise in jedem Optimierungsschritt ein kleines Loch an jener Stelle einfügen, an der die topologische Ableitung den größten Wert annimmt. Ähnlich kann man mithilfe der Formableitung in jeder Iteration ein Vektorfeld bestimmen, sodass eine Verformung des Gebiets in Richtung des Vektorfelds eine Verbesserung des Zielfunktionals nach sich zieht.
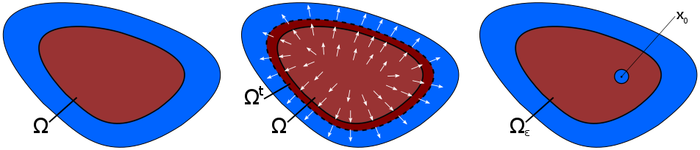
Abbildung 3: Schematische Darstellung einer Menge Ω, die den Eisenteil des Motors repräsentiert (links). Verformung von
Ω in Richtung eines Vektorfelds (Mitte). Veränderung von Ω durch Einfügen eines Loches (rechts).
Abbildung 4 (rechts) zeigt das Ergebnis einer Kombination dieser beiden Zugänge. Ausgehend vom Design in Abbildung 4 (links) werden die Designgebiete so modifiziert, dass die Laufruhe des Motors maximiert wird. Wir sehen, dass sich auf diese Weise ohne elektrotechnisches Vorwissen nur mithilfe geometrischer Ableitungsinformation neue, optimierte Maschinendesigns finden lassen. Für praktische Anwendungen in der Industrie müssten jetzt noch einige weitere Faktoren berücksichtigt werden. So reicht es üblicherweise nicht, für die Optimierung nur eine Zielfunktion zu betrachten. Beispielsweise müssen neben elektromagnetischem Verhalten auch die Kosten des Motors berücksichtigt werden. Es gibt dann nicht eine optimale Lösung, sondern eine Menge von Pareto-optimalen Designs. Weitere Faktoren sind mechanische Festigkeit, thermisches Verhalten und auch die Produzierbarkeit des Designs. Außerdem soll das im Computermodell erstellte optimale Design in der Realität robust gegenüber kleinen Abweichungen, wie sie etwa bei der Fertigung auftreten, sein. Das Thema der Optimierung elektrischer Maschinen kann also als ein mathematischer Spielplatz gesehen werden, der eine Vielzahl mathematischer und technischer Disziplinen miteinander verbindet und noch genügend Herausforderungen für weitere mathematische und interdisziplinäre Forschung zu bieten hat.

Abbildung 4: Anfangsgeometrie (links) und optimierte Geometrie (rechts) mit maximaler Laufruhe.

