In einer derartigen Datenflut wird es allerdings immer schwieriger, die richtigen Schlüsse zu ziehen und relevante Informationen herauszufiltern. In meiner Forschung versuche ich, Lösungsansätze zu Teilen dieser komplexen Problematik zu liefern.
Im Laufe der letzten Jahrzehnte wurde das Sammeln und Speichern von Daten ständig einfacher und preisgünstiger. In unserem alltäglichen Leben, aber auch in der Wissenschaft, gibt es viele Bereiche, wo Daten in hoher Auflösung gesammelt werden. Zum Beispiel können auf modernen Motorenprüfständen pro Sekunde mehrere Beobachtungen erhoben werden, und das für etliche Messgrößen gleichzeitig. Ähnliche Beispiele gibt es in vielen anderen Bereichen, man denke an Schadstoffmessreihen, hochfrequente Finanztransaktionen, funktionelle Magnetresonanztomografie etc. Um aus dieser Datenflut einen Nutzen zu ziehen, braucht es entsprechende statistische Methoden, die gewisse Problemstellungen auf das Wesentliche zu reduzieren vermögen und relevante Information extrahieren können. Die funktionale Datenanalyse (FDA) ist ein aufstrebendes Teilgebiet der Statistik, das sich mit dieser Problematik befasst. Methoden der FDA sind dann anwendbar, wenn jede einzelne Beobachtung eine auf einem Kontinuum definierte Funktion darstellt, zum Beispiel die Grauwerte in einem Schwarz-Weiß-Bild oder die Temperaturverteilung auf der Erdoberfläche, siehe Abbildung 1.
Wachstumskurven und PM10
Zur Illustration geben wir zwei einfache Beispiele: Wir betrachten zum einen Wachstumskurven von zehn Kindern im Alter von 0 bis 18 Jahren und zum anderen tägliche Feinstaubkurven in Graz an zehn aufeinanderfolgenden Wintertagen, siehe Abbildung 2. Jede dieser Kurven enthält eine Reihe von abstrakten Eigenschaften, die je nach Fragestellung relevant sein können: Zum Beispiel sind das Tagesmittel, das Maximum, ein eventueller Tagestrend oder die Zeitpunkte und die Anzahl von Spitzenwerten interessanter Kenngrößen für PM10-Daten. Wenn wir nicht nur am Verlauf eines einzelnen Tages interessiert sind, sondern vielmehr an einer zugrundeliegenden Systematik, bieten sich statistische Methoden an.
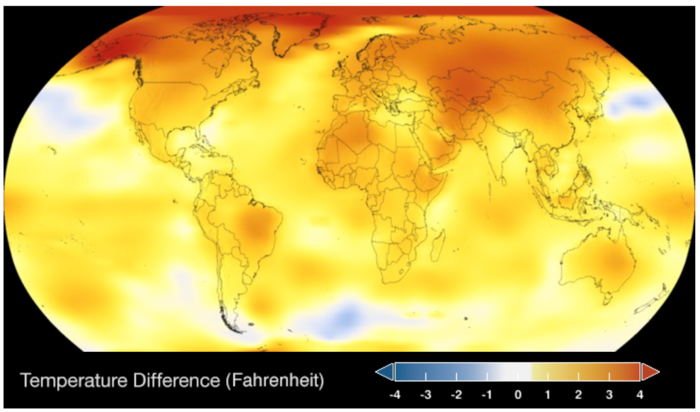
Veränderung der globalen Oberflächentemperatur gegenüber 1951–1980.
Anhand von wiederholten Messreihen (Wachstumskurven von Individuum 1, 2, 3 ... und Feinstaubbelastung an den Tagen 1, 2, 3 ...) versuchen wir, typische Muster zu erkennen. Im Idealfall können wir daraus Rückschlüsse auf die Schadstoffquellen ziehen oder Prognosen zum weiteren Wachstumsverlauf eines Kindes liefern. In beiden Beispielen gibt es eine natürliche Variation zwischen den Beobachtungen, die aus der Komplexität der zugrundeliegenden physikalischen und biologischen Prozesse rührt. Genau dann, wenn ein System zu komplex für ein exaktes naturwissenschaftliches Modell ist, helfen Methoden der Statistik und Wahrscheinlichkeitstheorie, um diese Variation zu modellieren
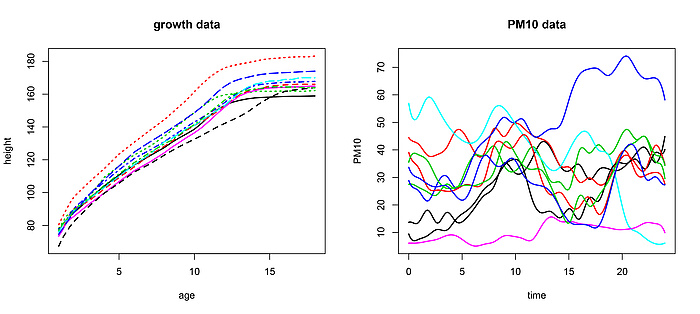
Zehn Wachstumskurven (linke Tafel) und zehn tägliche PM10-Stufen (rechte Tafel).
Umgang mit hoher Dimension
Aus mathematischer Sichtweise sind unsere funktionalen Beobachtungen Realisierungen eines stochastischen Prozesses. Da, wie oben angedeutet, die Trajektorien dieser Funktionen viele Eigenschaften besitzen, sind sie aus mathematischer Sicht hochdimensionale (theoretisch gesehen gar unendlichdimensionale) Objekte. Es ist also aus vielerlei Hinsicht wünschenswert, deren Dimension zu reduzieren und für die weitere Analyse nur die wichtigsten Eigenschaften herauszufiltern. Eine fundamentale Rolle spielt in diesem Zusammenhang die funktionale Hauptkomponentenanalyse. Hauptkomponenten sind orthogonale Funktionen. Durch Überlagerung dieser Funktionen lässt sich die ursprüngliche Funktion rekonstruieren. Man nennt dieses Verfahren Karhunen-Loève-(KL-)Entwicklung – ein Konzept, dessen theoretische Erforschung bereits Anfang des 20. Jahrhunderts stattfand. Zu diesem Zeitpunkt war eine statistische Anwendung nicht von Interesse, zumal es keine Möglichkeit einer numerischen Implementierung gab. Heute gibt es dazu Softwarepakete und wir können mittels einer KL-Entwicklung die Trajektorien unserer funktionalen Daten in beliebiger Dimension blitzschnell approximieren. Wer mit Fourierreihen vertraut ist, kann diese Methodik mit der Fourier-Entwicklung vergleichen. Hier werden Funktionen als Überlagerung von Sinus- und Cosinusschwingungen dargestellt. Der Vorteil der Hauptkomponenten liegt vor allem darin, dass sich diese in einem gewissen Sinne optimal an die Daten anpassen und damit eine ausgezeichnete Approximation bereits in kleiner Dimension gewähren. In Abbildung 3 illustrieren wir die Approximation eines PM10-Tagesverlaufs mit drei Hauptkomponenten bzw. mit 5 und 25 Fourier-Basen.
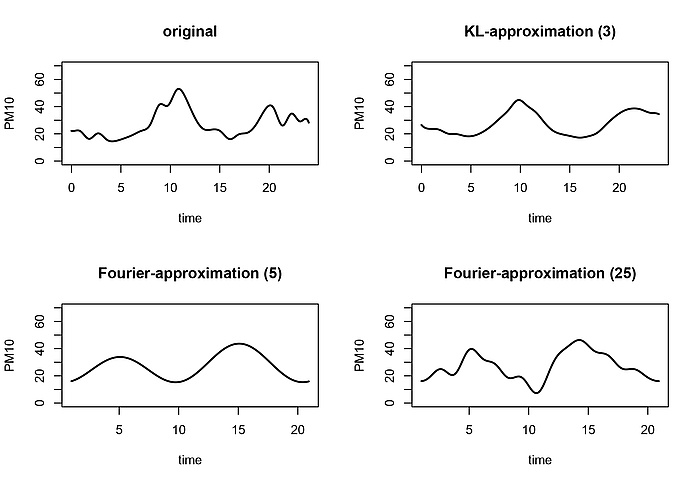
PM10-Kurve (oben links) und Approximation mit drei Hauptkomponenten (oben rechts). Die unteren Abbildungen zeigen die Approximation um fünf (links) und 25 (rechts) Fourier-Basisfunktionen.
Einbindung von serieller Abhängigkeit
Beim Vergleich von PM10- und Wachstumskurven fallen schnell einige offensichtliche Unterschiede auf. Zum Beispiel sind Wachstumskurven, im Gegensatz zu den PM10-Kurven, monoton und sehr glatt. Ein anderer wesentlicher Unterschied ist, dass die Wachstumskurven statistisch unabhängig sind: Der Verlauf des Wachstums eines Kindes hat keinen Einfluss auf den eines anderen Kindes. Für die PM10-Daten gilt dies nicht. Wenig überraschend gibt es starke Korrelationen zwischen den aufeinanderfolgenden Tagen. Im Zusammenhang mit FDA treten solche zeitlichen Abhängigkeiten sehr häufig auf.
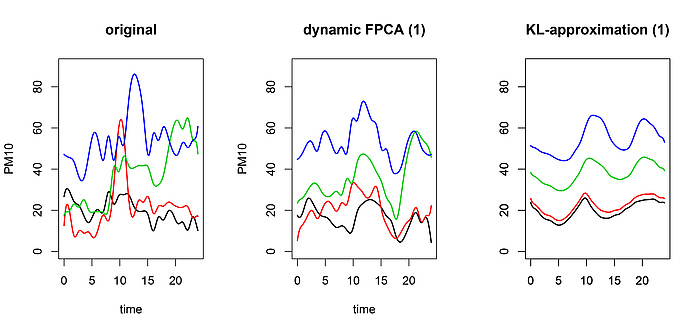
Vier PM10-Kurven (links) und Approximation durch eine dynamische Hauptkomponente (Mitte) sowie eine normale Hauptkomponente (rechts).
In einem meiner Forschungsprojekte zeige ich mit meinen Kolleg/innen, wie etwaige serielle abhängigkeit genutzt werden kann, um die Dimension von funktionalen Daten noch effizienter zu reduzieren. Unsere Methode heißt dynamische Hauptkomponentenanalyse und basiert auf frequenz-analytischen Methoden. Aus diesem Ansatz ergeben sich nebst verbesserter Interpretation der Daten etliche Anwendungen zur vereinfachten statistischen Inferenz. Zur Illustration vergleichen wir die Approximation von vier PM10-Kurven mit einer einzigen Hauptkomponente sowie mit einer einzigen dynamischen Hauptkomponente, siehe Abbildung 4.

