Umso erstaunlicher erscheint es, dass die Plastizität von Metallen bis heute ein nur unzureichend verstandenes Phänomen ist. Während elastische Materialeigenschaften von nicht zu komplexen Metalllegierungen heute mithilfe von quantenmechanischen Simulationen vorhergesagt werden können, gibt es noch keinen Weg, das plastische Verhalten aus grundlegenden Materialeigenschaften auf Kristallebene vorherzusagen.
Bleibende und damit plastische Verformungen von Kristallen entstehen durch die Bewegung linienhafter Defekte in der Kristallstruktur, die Versetzungen. Die Bewegung einzelner Versetzungen infolge von Spannungen im Material ist zumindest hinsichtlich einige Kristallklassen bereits gut verstanden. Allerdings enthalten die meisten Metalle sehr viele Versetzungen. In einem Kubikmillimeter Metall finden sich zwischen 1 und 10.000 km (!) Linienlaäge von Versetzungen. Insbesondere in Metallen mit kubischflächenzentrierter Kristallstruktur (zum Beispiel austenitische Stahle und Aluminiumlegierungen) sind daher weniger die Eigenschaften der einzelnen Versetzung als vielmehr das kollektive Verhalten einer großen Zahl von Versetzungen bestimmend für die plastischen Eigenschaften. Aus kollektiven Effekten resultiert dabei sowohl das Verfestigungsverhalten von Metallen bei plastischer Verformung als auch die Ausbildung charakteristischer Versetzungsstrukturen, die insbesondere bei dauerhafter Wechselbelastung zur sogenannten Materialermüdung und damit zum Versagen von Bauteilen führen können.
Kontinuumstheorie
In vielen physikalischen Zusammenhängen (Diffusion, Fluidmechanik, Plasmaphysik etc.) können Kontinuumstheorien mithilfe der statistischen Mechanik und Thermodynamik mit dem Verhalten einer Großzahl von Einzelobjekten und ihrer Wechselwirkungen verknüpft werden. Eine solche Verknüpfung galt in der Plastizitatstheorie noch bis vor Kurzem als aussichtslos. Als eine wesentliche Hürde auf dem Weg zu einer Kontinuumstheorie der Versetzungen wurde schon vor Jahrzehnten die Tatsache identifiziert, dass Versetzungen bewegliche und flexible Kurven sind. Daher können die Methoden der Teilchenphysik nicht ohne Weiteres angewandt werden.
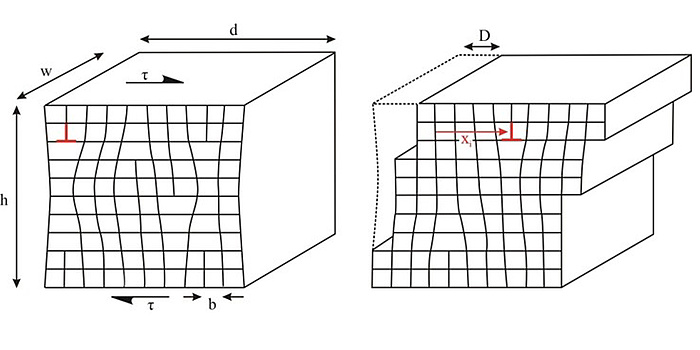
Schematische Darstellung der permanenten Scherung eines Kristalls, hervorgerufen durch die Bewegung sogenannter Stufenversetzungen.
Durch die Übertragung des Konzepts der Ausrichtungstensoren auf Verteilungen von Versetzungen und der Ableitung von Erhaltungsgleichungen fur diese Tensoren hat Thomas Hochrainer, Institut für Festigkeitslehre der TU Graz, kürzlich die Grundlage geschaffen, um die Kinematik der Versetzungsbewegung in einer versetzungsbasierten Kristallplastizitatstheorie zu erfassen. Im Rahmen der von der Deutschen Forschungsgemeinschaft geförderten Forschergruppe „Dislocation based plasticity“ mit interdisziplinaren Partnerinnen und Partnern am Karlsruher Institut für Technologie (KIT), der Friedrich-Alexander- Universitat Erlangen-Nürnberg und der Technischen Universität Bergakademie Freiberg arbeiten wir nun daran, in der Dichtetheorie kollektive Effekte durch Wechselwirkungen von Versetzungen zu berücksichtigen. Dazu werden Methoden der statistischen Mechanik und Thermodynamik von Vielteilchensystemen auf Versetzungssysteme ubertragen.
Dichtediagramm der Versetzungsdichte zu Beginn der Strukturbildung. Hellgrau bedeutet niedrige und Dunkelgrau hohe Dichte. Die Paare orthogonaler roter Doppelpfeile zeigen die lokale Ausrichtung der Versetzungen an.
Zu unserer Überraschung führt die Berücksichtigung von Wechselwirkung automatisch zu einer Tendenz zur Ausbildung von Versetzungsstrukturen. Der Grund ist, dass bestehende Inhomogenitäten durch eine Art Verkehrsstaueffekt verstärkt werden: Da, wo der Versetzungsfluss bereits durch ein hohe Dichte von Versetzungen behindert ist, werden ankommende Versetzungen gebremst und tragen zur weiteren Akkumulation und damit zur Verstärkung der Bremswirkung bei.
Elastische Wechselwirkungen begrenzen die Akkumulation und führen zu typischen Abmessungen der Strukturen. Die Abmessungen der aus der Kontinuumsversetzungsdynamik vorhergesagten Strukturen skalieren dabei wie experimentell erwartet mit dem mittleren Versetzungsabstand und invers zur anliegenden Spannung.
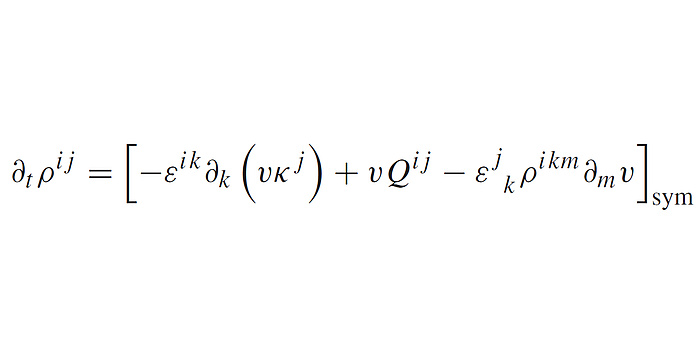
Entwicklungsgleichung des Versetzungsausrichtungstensors zweiter Stufe.
Durch die Berücksichtigung von Wechselwirkungen wird die resultierende Kontinuumsversetzungstheorie außerdem größenabhängig. Das bedeutet, dass für Probengrößen oder Bauteile, deren äußere Dimensionen in der Größenordnung des mittleren Versetzungsabstands sind, die plastischen Eigenschaften von der Größe des Objekts abhängen. Während die klassische Plastizitatstheorie keine Größeneffekte kennt, wurden Größenabhängigkeiten fur die Plastizität auf kleinen Skalen vielfach experimentell nachgewiesen. Wir sind derzeit dabei, die Kontinuumsversetzungstheorie durch Vergleich mit Mikrotorsionsversuchen am KIT zu validieren.
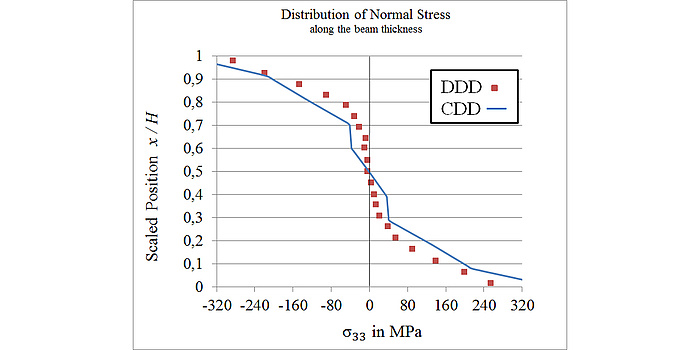
Längsnormalspannung in einem Mikrobalken unter Biegung. Durchgehende Linie: berechnet mit Kontinuumsversetzungsdynamik. Rote Symbole: Ergebnis einer diskreten Versetzungsdynamiksimulation am KIT.
Zukünftige Herausforderung
Als nächste große Herausforderung fur die Kontinuumsversetzungsdynamik bleibt die Vorhersage der Verfestigung. Hier entstehen neue theoretische Herausforderungen, da sich durch sogenannte Versetzungsreaktionen die Topologie der Versetzungsnetzwerke laufend verändert, was in den bestehenden Entwicklungsgleichungen noch nicht berücksichtigt wird.
Dieses Forschungsgebiet ist im FoE „Advanced Materials Science“ verankert, einem der fünf Stärkefelder der TU Graz.
