Adaptierung und numerische Implementierung eines Phasenfeldmodells zur chemo-mechanischen Mikrostrukturanalyse der Leerstellendiffusion
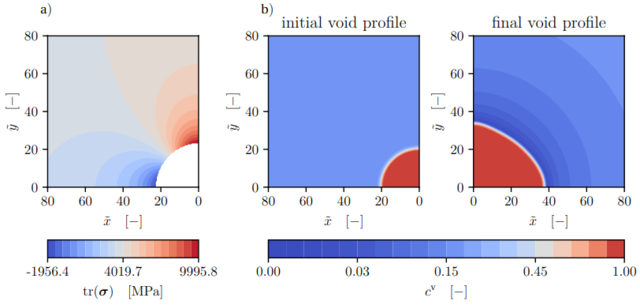
Phasenfeldmodelle haben sich in der Mikrostrukturanalyse als besonders nützlich erwiesen, da sie die Behandlung freier (Phasen-)Ränder erleichtern und komplexe Phasenübergänge ohne explizite Randverfolgung beschreiben können. Dabei werden mathematisch scharfe Ränder "verschmiert", wodurch eine diffuse Übergangszone entsteht, die Teil des zugrundeliegenden Anfangsrandwertproblems wird. Dieser Ansatz wurde in einem chemo-mechanischen Modell zur Analyse der Diffusion von Leerstellen (Punktdefekten), die zu Poren aggregieren können (=Phasenübergang Material zu Pore), verwendet [1]. Bei der elastischen Kopplung dieses Modells wurden numerische Artefakte des Spannungsfelds in der Grenzschicht durch das Verknüpfen der zugrundeliegenden Diffusionsvariablen unter Kontrolle gebracht. Eine alternative Lösung für dieses Problem könnte die Umformulierung des bestehenden Modells nach Kim-Kim-Suzuki [2] (KKS) sein, welches hauptsächlich für binäre Systeme (Legierungen) verwendet wird. Das KKS Modell basiert auf der Gleichheit der chemischen Potentiale in der Grenzschicht und bietet eine realistischere Darstellung der Phasengrenzen und ihrer Dynamik sowie eine bessere numerische Stabilität. Allerdings stellen Logarithmusterme, die nur für strikt positive Werte definiert sind und zur Beschreibung entropischer Zusammenhänge verwendet werden, weiterhin eine Herausforderung dar.
Im Zuge der Masterarbeit soll das oben erwähnte Phasenfeldmodell aufbereitet und in das Framework MOOSE [3] implementiert werden. MOOSE besitzt zum einen Kernels für Kim-Kim-Suzuki Modelle und zum anderen Funktionen, die den Umgang mit Logarithmen numerisch regeln. Die Umsetzbarkeit und das Verhalten des neu entwickelten Modells für verschiedene Parameter im Vergleich zum ursprünglichen soll untersucht werden, sowie dessen Auswirkungen auf die mechanische Kopplung soll analysiert und diskutiert werden.
[1] K. A. Pendl and T. Hochrainer. Coupling stress fields and vacancy diffusion in phase-field models of voids as pure vacancy phase. Comput. Mater. Sci., 224 (2023)
[2] S. G. Kim, W. T. Kim, and T. Suzuki. Phase-field model for binary alloys. Phys. Rev. E 60 (1999)
[3] D. Schwen et al. Rapid multiphase-field model development using a modular free energy based approach with automatic differentiation in MOOSE/MARMOT. Comput. Mater. Sci., 132 (2017)
Aufgaben:
• Literaturrecherche Phasenfeldmethode (insbesondere Leerstellendiffusion, KKS-Modell, WBM-Modell, mechanische Kopplung, MOOSE)
• Erstellen einfacher, erster Implementierungen („Referenzmodell“: ggf. mit MATLAB oder Python) bzw. Durchsicht und Analyse vorhandener KKS Modelle in MOOSE
• Herleitung und Analyse relevanter Gleichungen
• Implementierung des neu formulierten Modells in MOOSE
• Validierung der Algorithmen, Analyse und Dokumentation der Ergebnisse
• Optional: Herleitung, Implementierung und Diskussion mechanischer Kopplung für große Deformationen
Was Sie mitbringen sollen:
• Lehrveranstaltungen „Höhere Festigkeitslehre“ (VO und/oder UE) von Vorteil, optional LVs wie „Laborübung FE-Methoden“, oder „Rechnerübung Nichtlineare Festkörpermechanik“
• Interesse an Festkörpermechanik und gekoppelten Problemstellungen
• Programmiererfahrung (mit einer beliebigen Programmiersprache) vorteilhaft
Was wir Ihnen bieten:
• Intensive Betreuung am Institut
• Einarbeiten in numerische Algorithmen und Anwenden von theoretischem Wissen
Beginn: ab sofort möglich
Kontakt: Dipl.-Ing. Kevin Pendl BSc kevin.pendl@tugraz.at
