Antwort: Nein, sie sind von der Querschnittsform abhängig
Erklärung
Merkmal zum Verlauf der Verwölbungen
- Sie sind von der Querschnittsform abhängig
- Bei konstantem Stabquerschitt bleibt der Verlauf der Verwölbungen, infolge einer Einheitsverdrillung, in jedem Querschnitt gleich - unabhängig von der Lage x am Stab
- Die Querschnitte lassen sich klassifizieren in wölbfreie, quasi wölbfreie und Querschnitte mit Verwölbung
- Kastenquerschnitte weisen mitunter Verwölbungen auf, die jedoch meist vernachlässigbar klein bleiben ("quasi wölbfrei")
wölbfrei
Wölbfrei ist der Kreisquerschnitt, der Kreisringquerschnitt, alle dünnwandigen Querschnitte deren Querschnittsteile sich in einer Achse schneiden und der quadratische Kasten mit konstanter Wanddicke.
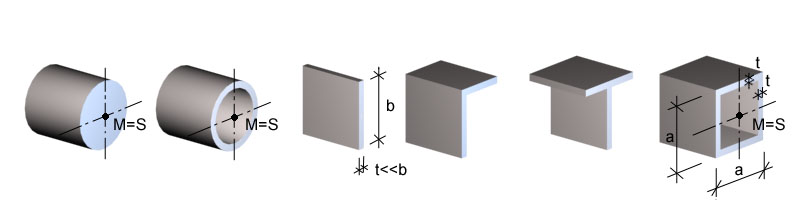
quasi wölbfrei
Alle geschlossenen Querschnitte (hier an einzelligen Querschnitten dargestellt) können vereinfacht als wölbfrei angesehen werden, da die St. Venant´sche Torsion dominiert. Bei Einhaltung der dargestellten Zusatzbedingung sind sie tatsächlich wölbfrei.
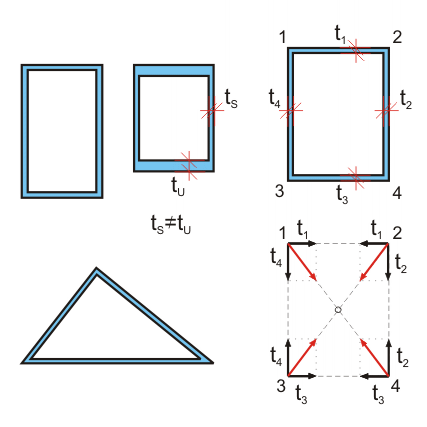
Zusatzbedingung für wölbfrei:
- fasse Wanddicken ti als Vektoren auf, die in den Eckpunkten mit ihren Resultierenden eingetragen werden. Schneiden sich die Resultanten in einem Punkt - folgt ein wöbfreier Querschnitt
- dies gilt für alle einzelligen Kastenquerschnitte (Dreiecke, Polygone)
nicht wölbfrei (mit Verwölbungsverlauf ui)
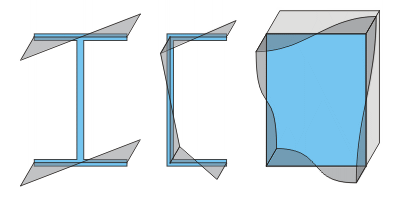

 Zusatzbedingung für wölbfrei:
Zusatzbedingung für wölbfrei: