Torsionsbeanspruchung M_x - notwendige Trennung in 2 Anteile

Gesamtbeanspruchung M_x = St. Venant´sche Torsion (M_xp) + Wölbkrafttorsion (M_xs) Anmerkung: Diese Bezeichnung ist vielfach in der Literatur zu finden.

• Index p ... primär
• Index s ... sekundär

Im Gegensatz zur St. Venant´schen Torsion existieren bei der Wölbkrafttorsion Nomalspannungen, die den Schubspannungen das Gleichgewicht halten (ähnlich wie im Kapitel "Schubspannungen aus Querkraft" gezeigt). Bei der St. Venant´schen Torsion ist dies nicht der Fall.

St. Venant´sche Torsion

Der Verlauf der Schubspannung über die Dicke ist linear veränderlich. Zunächst werden die beiden resultierenden Schubflüsse Ti* berechnet. Der Hebelarm ist der Abstand zur Profilmittellinie. Das Moment berechnet sich, indem der Schubfluß Ti* multipliziert mit dem Hebelarm über das gesamte Profil aufsummiert wird.

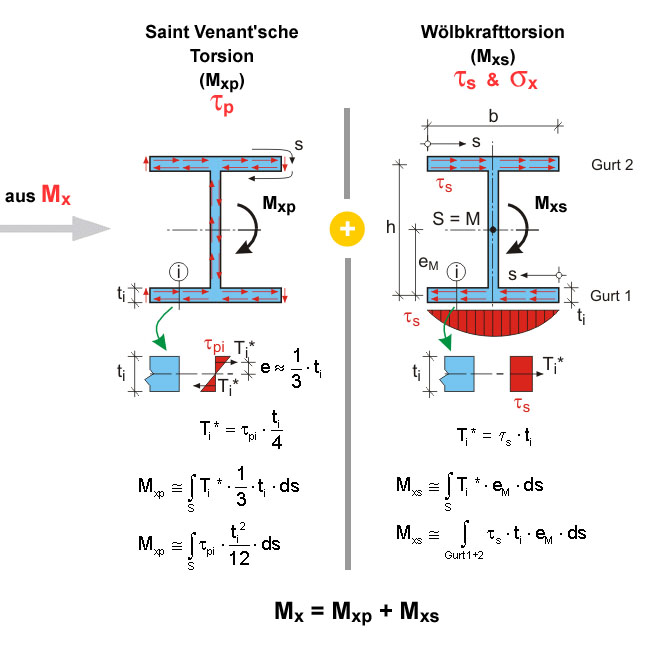
Wölbkrafttorsion

Der Verlauf der Schubspannungen über die Dicke ist konstant. Der Hebelarm ist der Abstand des Gurtes vom Schubmittelpunkt M. Das Moment berechnet sich, indem der Schubfluß Ti* multipliziert mit dem Hebelarm über beide Gurte aufsummiert wird. Beachte: bei den dargestellten offenen Querschnitten ist die Wandstärke ti viel kleiner als der Gurtabstand eM - deshalb sind bei gleichmäßiger Aufteilung des am Querschnitt wirksamen Torsionsmomentes (Mxp = Mxs) die primären Schubspannungen somit wesentlich höher als die sekundären Schubspannungen.

› weiter