2. Geschlossene dünnwandige Querschnitte

2.1 Spannungsverlauf - allgemein

Merkmal

• Gleichgewichtsbedingung alleine unzureichend
• zusätzliche Verträglichkeitsbedingung der Verwölbungen notwendig

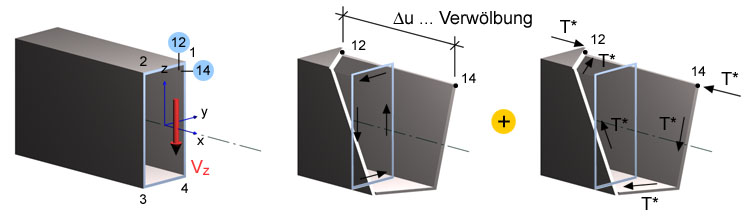
  Bisher wurden nur offene Querschnitte behandelt. Zur Berechnung der Schubspannungen der geschlossenen Querschnitte sind jedoch nicht mehr die Gleichgewichtsbedingungen ausreichend. Es handelt sich somit um ein statisch unbestimmtes Problem. Die Berechnung erfolgt mit dem Kraftgrößenverfahren (analog einem statisch unbestimmten Biegeträger).

Vorgehen

Zunächst wird der Querschnitt an der Kante 1 aufgeschnitten. Dies verletzt die Verträglichkeit, was durch eine statisch unbestimmte Kraftgröße X wieder rückgängig gemacht werden muss (hier Schubfluß T*). Es entsteht ein statisch bestimmter offener Querschnitt (analog zu Biegeträger: Einfügen eines Gelenks, Wegschneiden eines Auflagers). Im nächsten Schritt wird die Verteilung des Schubflusses am nun offenen Querschnitt zufolge der Querkraft V_z und des statisch unbestimmten Schubflusses T*=1 berechnet. Daraus ergibt sich mit Hilfe des Prinzips der virtuellen Verschiebung die Verformung in Richtung des fiktiven Schnitts in der Kante 1. Aus der Verträglichkeitsbedingung (Klaffung in Kante 1 muss verschwinden) ergibt sich der statisch unbestimmte Schubfluß T*.

• je Einzelzelle 1 Unbestimmte T*

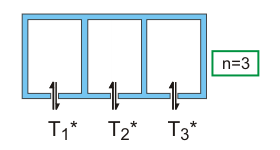
Ein mehrzelliger Querschnitt ist ein mehrfach statisch unbestimmtes System. Es ergeben sich mehrere statisch unbestimmte Schubflüsse T*. Durch Ausnutzung der Symmetrie kann am halben System gerechnet werden.

› weiter