4. Ingenieurpraktisches Zahlenbeispiel
Kragträger mit starrer Einspannung
Der Unterschied zum vorherigen Beispiel ist, dass hier an der Einspannstelle die Verwölbung gesperrt ist. Das Torsionsmoment wird hier nun zum Teil auch über die Wölbkrafttorsion abgetragen. Anmerkung: Der Kastenquerschnitt B wird hier nicht weiter verfolgt, da der Wölbkrafttorsionsanteil nur in einem kurzen Bereich um die Einspannstelle bedeutsam ist. In der Praxis wird dieser Anteil meist vernachlässigt.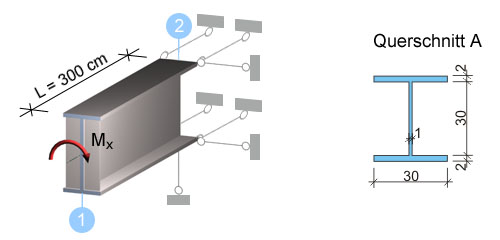 Es erfolgt eine ingenieurmäßige Betrachtung der beiden Grenzfälle:
Es erfolgt eine ingenieurmäßige Betrachtung der beiden Grenzfälle:- alleinige Lastabtragung über St. Venant´sche Torsion (Fall 1). Die Ergebnisse entsprechen jenen des bereits dargestellten Kragträgers mit Gabellagerung.
- alleinige Lastabtragung über Wölbkrafttorsion (Fall 2). Dies wird im Folgenden gezeigt.
Frage a): Grenzfallbetrachtung
Antwort:
Querschnitt A
- Interaktion zwischen St. Venant´scher Torsion und Wölbkrafttorsion; Verhältnis Mxp / Mxs in Längsrichtung veränderlich
- vereinfachte ingenieurmäßige Betrachtung ist nur für die beiden folgenden Grenzfälle möglich:
- Fall 1: nur St. Venant´sche Torsion - daraus folgt Mxp = Mx
- Fall 2: nur Wölbkrafttorsion - daraus folgt Mxs = Mx
- Aus dem Vergleich der Verformungen (horizontale Gurtverformung vG am Kragende) beider Grenzfälle ist abschätzbar welcher Anteil überwiegt bzw. es ist die reale Aufteilung in beide Anteile grob abschätzbar.
Fall 1: nur St. Venant´sche Torsion
- τmax = 11.8 kN/cm2
- max. Gurtverschiebung (horizontal) : vG = 3.5 cm
Fall 2: nur Wölbkrafttorsion
- Isolierte Betrachtung jedes Gurtes möglich (Horizontalbiegung)
- Hy = Mx / eG = 10 / 0.32 = 31.3 kN. Nunmehr kann jeder Gurt isoliert als Biegeträger mit Rechteckquerschnitt betrachtet werden (System: Kragträger). Damit ergeben sich die dargestellten Verläufe für Querkraft V und Biegemoment M in den Gurten. Die Spannungsermittlung für V und M erfolgt wie für den Rechteckquerschnitt.
- Spannungen am Querschnitt
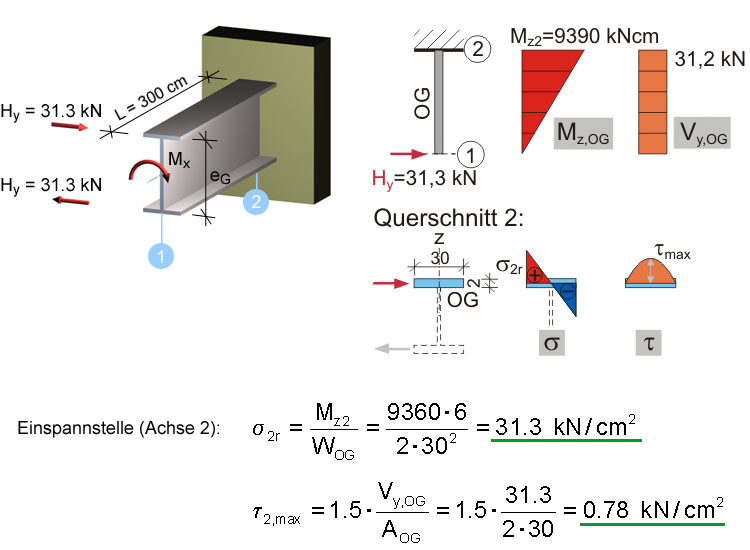 Wegen V = konst. sind die Schubspannungen in allen Querschnitten gleich, wogegen die Biegenormalspannungen, zufolge der Zunahme des Biegemomentes, in den Querschnitten zunehmend von 1 nach 2 gehend, größer werden.
Wegen V = konst. sind die Schubspannungen in allen Querschnitten gleich, wogegen die Biegenormalspannungen, zufolge der Zunahme des Biegemomentes, in den Querschnitten zunehmend von 1 nach 2 gehend, größer werden.