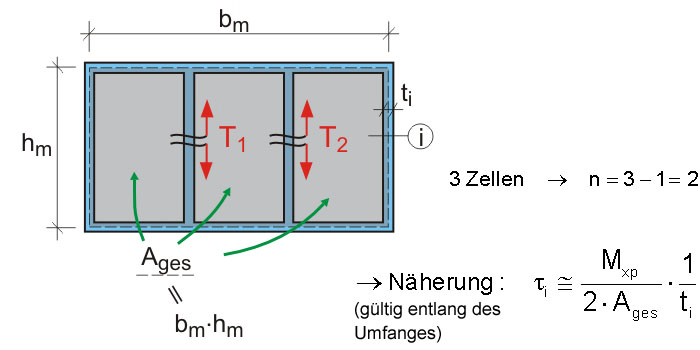
Dünnwandiger, mehrzelliger Kastenquerschnitt

Der einzellige Querschnitt ist statisch bestimmt. Für jede weitere Zelle erhöht sich die Zahl der statisch Unbestimmten um eins. Die Berechnung erfolgt mit dem Kraftgrößenverfahren (Vergleich: Schubspannungen aus Querkraft am geschlossenen Querschnitt). Bei mehrzelligen Querschnitten ist der Grad der statischen Unbestimmtheit bei Torsionsmomenten im Vergleich zur Querkraftbeanspruchung um eins niedriger, da bei Torsion der einzellige Querschnitt statisch bestimmt ist, jedoch bei Querkraft der offene Querschnitt. Der Schubfluß in den Innenwänden ist sehr gering. Als Näherung kann daher nur am einzelligen Querschnitt, bestehend aus den Außenwänden, gerechnet werden.
  • zusätzliche Verträglichkeitsbedingungen zur Ermittlung des Schubspannungsverlaufes - daraus folgt Anzahl n der Unbekannten = Gesamtzellenanzahl -1.

Sonderfall: 2-zelliger Kasten einfachsymmetrisch

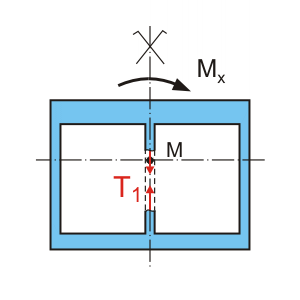
Frage:

Ermittlung der Schubspannungsresultante T1 der Zwischenwand. Ist T1 nur von der Querschnittsform abhängig?

Antwort: Τ1=0

Erklärung

  • Die Resultante Ti verläuft durch den Schubmittelpunkt M und kann daher keinen Beitrag zu Mx liefern, da der Schubmittelpunkt den Drehpunkt bei Torsion darstellt - daraus folgt T1 = 0.
  • Folgerung: Querschnitt kann wie einzelliger Kastenquerschnitt, ohne Zwischenwandung behandelt werden.

  › nächste Frage