Dünnwandiger, offener Querschnitt

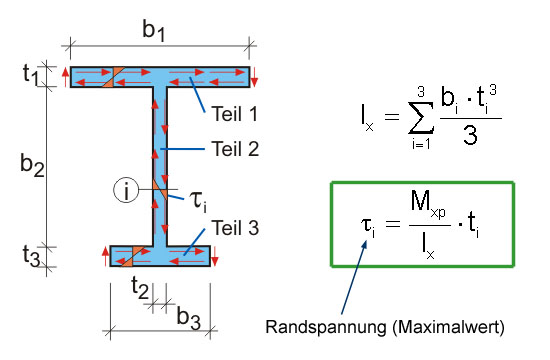
Merkmal

• Man stelle sich den Gesamtquerschnitt als Summe von Einzelrechtecken vor, für die wieder die Schubspannungsverteilung des Rechteckquerschnitts gilt. Das Gesamttorsionsmoment M_xp verteilt sich auf die einzelnen Rechtecke im Verhältnis ihrer Torsionsträgheitsmomente. Dies führt letztendlich auf die angegebene Formel, die keine Aufteilung erfordert.
• Schubspannungsrichtung am Querschnittsrand: Entspricht der Richtung bei Umlauf um die gesamte Querschnittskontur

Auch beim zusammengesetzten Querschnitt kann weiter mit der einfachen Formel gerechnet werden. Die Schubspannungen am offenen Querschnitt sind proportional zur Wanddicke. Die größten Schubspannungen treten daher an den dickeren Querschnittsteilen auf. Die Schubspannung verläuft linear veränderlich über die Dicke.

Dünnwandiger, einzelliger Kastenquerschnitt

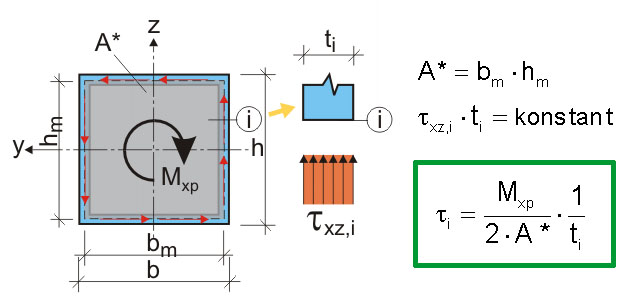
Merkmal

• Man stelle sich den Gesamtquerschnitt als geschlossene Ringleitung vor. Die Schubspannungen entsprechen den zirkulierenden "Wasserteilchen". Höhere Fließgeschwindigkeit bei kleinerer Wanddicke entspricht der Höhe der Schubspannung.

Beim geschlossenen Querschnitt hängt die Größe der Schubspannungen von der umschlossenen Fläche ab. Die Schubspannungen sind im Gegensatz zum offenen Querschnitt indirekt proportional zur Wanddicke. Die größten Schubspannungen treten daher an den dünneren Querschnittsteilen auf. Der umlaufende Schubfluß ist über den ganzen Querschnitt konstant. Der Verlauf der Schubspannungen ist konstant über die Dicke.

Erklärung

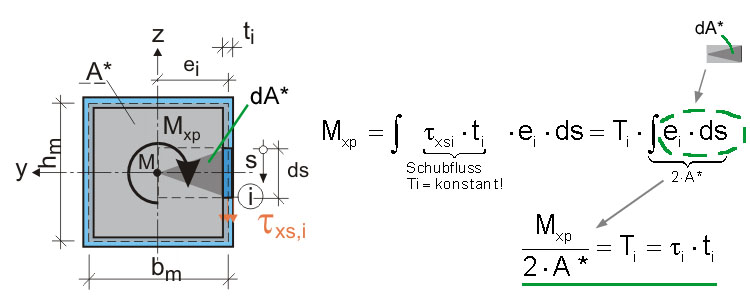
Beim geschlossenen Querschnitt ist das einwirkende Torsionsmoment gleich dem resultierenden Moment der Schubflüsse um den Schubmittelpunkt M. Dies führt auf das dargestellte Integral. Die Schubspannungen im Einzelblech werden als konstant angenommen, da der Abstand zu M groß gegenüber der Wanddicke ist. Das Integral entspricht der doppelten Fläche A*.

› weiter