Ableitung der Grundgleichung für τ_x,i - Sonderfall M_y nur in einer Schnittebene

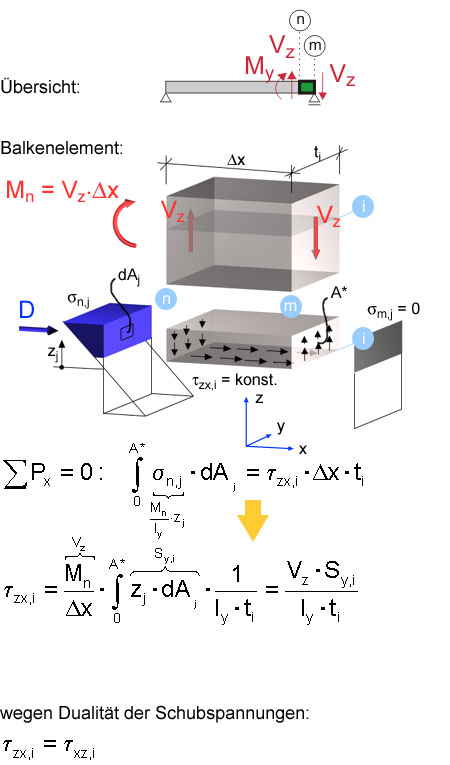
Zuerst erfolgt die Abtrennung eines kurzen Stabelements Δx mit den Schnittflächen m und n. Nun erfolgt die Abtrennung des "Oberteils" entlang der Schnittfläche i. Dieser Oberteil weist die Querschnittsfläche A* auf. An diesem freigeschnittenen "Oberteil" wird nun das horizontale Gleichgewicht in Stablängsrichtung gebildet. Dazu tragen die Normalspannungen in der Ebene n und die als konstant angesetzten Schubspannungen in der Schnittfläche i bei. Daraus ist die Größe der Schubspannungen ermittelbar. Die Dualität der Schubspannungen führt zu den gesuchten Schubspannungen der Querschnittsfläche m entlang der Schnittfläche i.

Grundgleichung für τ_x,i - allgemeiner Fall

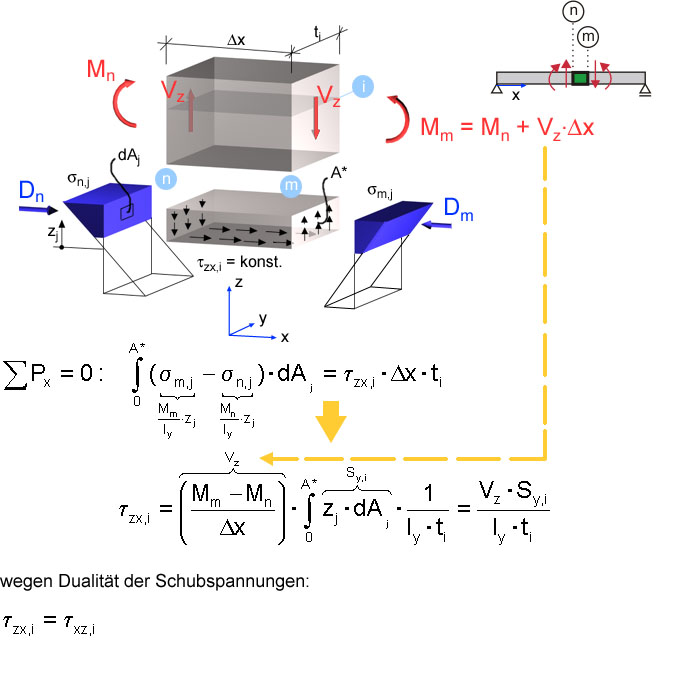
Grundgleichung gilt allgemein - auch bei (V_z + M_y) in jedem Querschnitt Ergänzend ist hier noch der allgemeine Fall (Biegebeanspruchung M_y auch in Schnittfläche m) dargestellt. Gegenüber dem oben gezeigten Fall sind nun auch die Normalspannungen in der Ebene m bei der Gleichgewichtsbetrachtung zu berücksichtigen.

zurück